• Vznik a raný vývoj
• Paradox Algolu
• Lagrangeovy body
• Hillovy plochy
• Výměna hmoty
• Střední hmotnosti
• Masivní dvojhvězdy
• Zdroje

Hillovy plochy jsou ekvipotenciální plochy, pro něž platí Φ(x,y)=konst., kde Φ je Hillův potenciál, který je kombinací gravitačního potenciálu a odstředivé síly. Okolo samostatného homogenního objektu mají tyto plochy tvar soustředných koulí, v jejichž společném středu je těžiště objektu. V případě nehomogenních těles nebo v případě více těles, se tyto plochy deformují. V soustavě dvojhvězdy mají význam pro pohyb těles okolo jednotlivých složek, ale i pro pohyb hmoty samotné hvězdy. Pohybuje-li se bod po ekvipotenciální ploše, nekoná práci, neboť se pohyb děje kolmo k působící síle. Jsou-li objekty, udržované pohromadě vlastní gravitací, složeny z plastického materiálu (může se pohybovat), pak v nich plochy se stejnou hustotou musí v rovnovážném stavu zaujímat tvar ekvipotenciálních ploch. Pokud hvězda v některé fázi svého vývoje zvětší svůj poloměr, bude její povrch sledovat zdeformované Hillovy plochy a bude se deformovat podle nich.

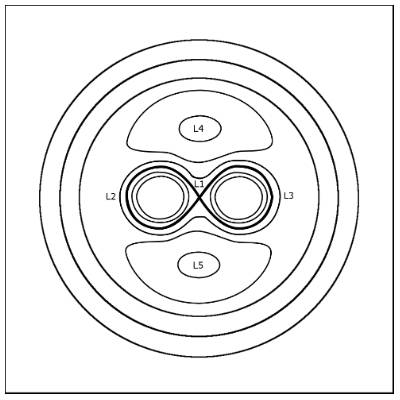
Na dalším obrázku je situace znázorněna pro soustavu dvojhvězdy, jejíž obě složky mají stejnou hmotnost. Při nestejné hmotnosti složek mění Hillovy plochy svůj tvar. Znázorněno je to na tomto appletu (www.aldebaran.cz), který počítá průběhy Hillových ploch na základě zadání hmotností obou složek.

Hillovy plochy v soustavě dvojhvězdy

Hillovy plochy se zde postupně deformují do kapkovitého tvaru. Hillova plocha, která je společná pro obě hvězdy a má společný jeden librační bod L₁, se nazývá Rocheova mez nebo Rocheova plocha. Na obrázku je vyznačena tlustou čarou a vytváří tak tvar osmičky. Kolem každé složky vytváří Rocheův lalok, který vymezuje chování hmoty a těles uvnitř. Těleso, které se nachází v Rocheově laloku jedné hvězdy podléhá jejímu gravitačnímu poli a obíhá okolo ní. Tělesa mimo Rocheovy laloky obíhají po složitých drahách, pokud jsou v blízkosti Rocheovy meze, nebo po kruhových drahách kolem hmotného středu soustavy, pokud obíhají ve větší vzdálenosti. Samy hvězdy okolo sebe obíhají téměř po kruhových drahách. I kdyby totiž při vzniku byly jejich dráhy eliptické, silné slapové působení mezi hvězdami způsobí pokles výstřednosti a přechod na kruhové trajektorie.

Geometrie Rocheových ekvipotenciál dle očekávání závisí pouze na poměru hmotností obou složek. Poněkud nečekaný je ovšem výsledek, že úhel, pod nímž se dotýkají špičky kritického Rocheova laloku v bodě L₁ prakticky nezávisí ani na tom poměru a činí asi 115°. Užitečný je aproximativní vztah pro vzdálenost Lagrangeova bodu L₁ od středu první složky l₁:

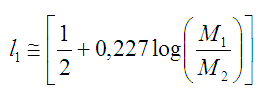
Tento vztah odvodili Plavec a Kratochvíl v roce 1964. Ačkoli Rocheův lalok nemá kulový tvar, lze definovat jistý poloměr Rocheova laloku R_L, který odpovídá poloměru koule o jeho objemu. Aproximační vztah odvodili Icko Iben a Alexandr V. Tutukov (1984):

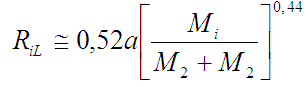
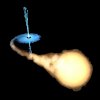
Pokud jedna hvězda v některé fázi svého vývoje zvětší svůj poloměr (například při přechodu do stádia rudého obra nebo při zapálení nových reakcí ve svém jádru), může její hmota, pohybující se po zdeformovaných Hillových plochách, dosáhnout až Rocheovy meze a vyplnit svůj Rocheův lalok. Hmota, která dosáhla Rocheovy, meze může uniknout z gravitačního vlivu mateřské hvězdy. Většina hmoty začne bodem L1 přetékat na druhou složku. K takovéto výměně může během vývoje dojít několikrát a může při ní být přenesena podstatná část hmoty soustavy. Při vyplnění obou Rocheových laloků může hmota začít unikat i body L₂a L₃.

Hvězdy se tedy mohou ovlivňovat nejenom svými gravitačními účinky, ale i přímo přetokem hmoty. Její výměna nejen že zasahuje do vývoje jednotlivých složek, ale ovlivňuje také jejich dráhové elementy.