Degenerovaný plyn

Degenerovaný plyn a druhy degenerace

Degenerovaný plyn je plyn, jehož odpor proti stlačování pochází největším dílem z Pauliho vylučovacího principu. Tlak proti stlačování se v případě degenerovaného plynu nazývá degenerovaný tlak a jeho nárůst je dán tím, že Pauliho vylučovací princip zakazuje fermionům okupovat v prostoru určeném Heisenbegovou relací neurčitosti stejný kvantový stav. Každý pokus o jejich dodatečné stlačení vyústí ve zvýšení jejich energetických hladin (zvýšení energie).

Představme si plazma, které nejprve ochlazujeme a poté stlačujeme. Celý postup opakujeme až do chvíle, kdy zjistíme, že plazma už nelze dále stlačit. V tomto momentě totiž narostl tlak díky zmíněnému Pauliho vylučovacímu principu. V tomto stavu, kdy objem stlačeného plazmatu je velmi malý, můžeme prohlásit, že poloha částic je s poměrně velkou přesností definována. Protože však Heisenbergovy relace neurčitosti říkají, že „neurčitost v prostoru vynásobená neurčitostí hybnosti je větší a nebo rovna Planckově konstantěπ“, docházíme k závěru, že hybnost takových přesně lokalizovaných částic musí být velmi vysoká. Jinak řečeno, i když je plazma studené, částice se stejně pohybují velkými středními rychlostmi. Chceme-li tedy dosáhnout dalšího stlačení, musíme vyvinout extrémně velkou sílu, která by dokázala překonat tlakovou sílu vyvolaný extrémní hybností částic.

Z hlediska částic, z nichž se skládá degenerovaný plyn, rozlišujeme elektronovou degeneraci (bílí trpaslíci) a neutronovou degeneraci (neutronové hvězdy).

Srovnání normálního a degenerovaného plynu

Ideální plyn

Představme si jednoatomový ideální plyn uzavřený v krabici (uvažujeme konstantní hmotnost plynu). Pro tlak, kterým bude plyn působit na stěnu, platí:

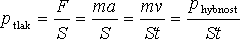(2.1)

F značí sílu, m hmotnost částice a v je její hmotnost.

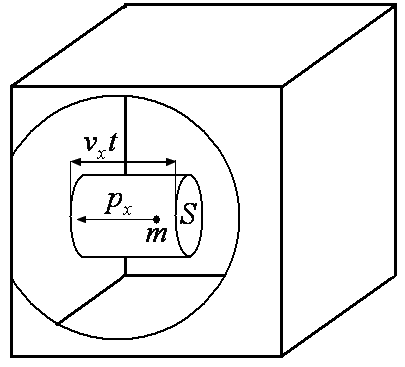
Pro hybnost přenesenou plochou S za čas t můžeme psát:

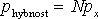(2.2)

N značí celkový počet částic pohybujících se podél osy x a p_x je jejich hybnost. Uvážíme-li objem vyznačeného válce na obrázku, mohu vztah (2.2) přepsat:

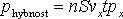(2.3)

Zde n značí počet částic v 1 m³, S je plocha podstavy válce, v_x je rychlost částice, t je čas. Dosadíme-li do rovnice (2.1) vztah (2.3), získáme:

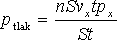(2.4)

S označuje plochy, můžeme je tedy zkrátit. Stejně tak se zbavíme i času t. Výsledkem je:

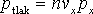(2.5)

Protože složka p_x při odrazu od stěny změní směr na opačný a zachová si svou velikost, bude celková hybnost dodaná stěně atomem při jedné srážce 2mv_x, tedy:

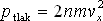(2.6)

Ne každý atom má stejnou rychlost a ne každý se pohybuje týmž směrem. Veličiny 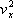jsou tedy pro každý atom různé. Musíme tedy vzít střední hodnotu z .

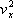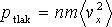(2.7)

Koeficient 2 z (2.6) můžeme vynechat, neboť ze všech atomů směřuje k pístu jen polovina. Ta druhá se pohybuje na opačnou stranu.

Směr osy x není nijak zvláštně preferován a atomy se narážejí stejně i v ostatních směrech. Proto bude střední hodnota 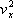rovna odpovídajícím středním hodnotám v ostatních dvou směrech, tedy:

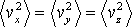(2.8)

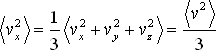(2.9)

Výhodou takového zápisu je, že se nemusíme starat o nějaký speciální směr a formule pro tlak získá tvar

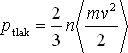(2.10)

Poslední činitel zapisuje ve daném tvaru proto, že taková je kinetická energie pohybu těžiště molekuly (atomu).

Nyní je třeba získat závislost tlaku na teplotě. Zde vyjdeme z ekvivalence kinetické energie pohybujících se částic plynu a vnitřní energie ideálního jednoatomového plynu.

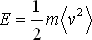(2.11)

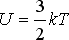(2.12)

kde k značí Boltzmanovu konstantu a T termodynamickou teplotu.

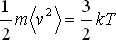(2.13)

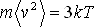(2.14)

Kombinací vztahů (2.10) a (2.14) dostáváme stavovou rovnici ideálního jednoatomového plynu. Zde n značí koncentraci (počet částic na m³).

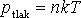(2.15)

Je patrné, že se zvýšením teploty se zvyšuje i tlak při konstantní koncentraci atomů.

Degenerovaný plyn

Pro degenerovaný plyn stavová rovnice ideálního plynu při určovaní tlaku nepomůže. Je to dáno tím, že v degenerovaném plynu hrají významnou roli kvantově-mechanické jevy, a to zejména zmiňovaný Pauliho vylučovací princip a Heisenbergovy relace neurčitosti.

Podle Heisenberovy relace neučitosti nelze současně změřit polohu a hybnost částice s větší přesností, než Planckova konstanta. Matematicky vyjádřeno:

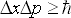(2.16)

Naše výchozí předpoklady jsou následující:

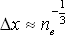(2.17)

kde n_e vyjadřuje počet elektronů na 1 m³. Znaménko vyjadřuje úměrnost (zanedbáváme pro jednoduchost číselné konstanty).

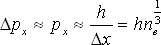(2.18)

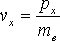(2.19)

Předpoklady (2.17), (2.18) a (2.19) dosadíme do rovnice (2.5), neboli:

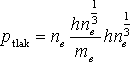(2.20)

Úpravou získáváme tlak degenerovaného elektronového plynu:

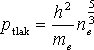(2.21)

Protože je používání počtu elektronů n_e poněkud nepraktické, přepočítáme výsledný vztah (2.21) na hustotu ρ. Naším dalším výchozím bodem bude předpoklad elektrické neutrality degenerovaného plynu. Počet elektronů musí být stejný, jako počet protonů. Protony jsou obsaženy v atomových jádrech o protonovém čísle Z. Platí:

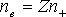(2.22)

kde n₊ značí počet atomových jader v 1 m³, n_e počet elektronů v 1 m³.

Hustota bude:

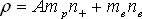(2.23)

V tomto vztahu předpokládáme, že hmotnost protonů je rovna hmotnosti neutronů. m_p označuje hmotnost protonu a A nukleonové číslo.

Jelikož je hmotnost elektronů ve srovnání s hmotností nukleonů zhruba 1 800krát menší, mohu jejich vliv na výslednou hustotu hmoty zanedbat a položit:

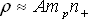(2.24)

Kombinací (2.24) a (2.22) dostaneme:

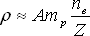(2.25)

Odtud:

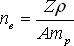(2.26)

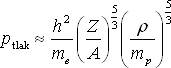(2.27)

Tento finální vztah (2.27) je pro nás velice důležitý. Vyplývá z něho, že tlak degenerovaného elektronového plynu na rozdíl od plynu ideálního (2.15) nezávisí na teplotě.