Trajektorie dvojhvězd – problém dvou těles
Pohyb dostatečně vzdálených hvězd o hmotnostech M1 a M2 ve dvojhvězdě lze v prvním přiblížení řešit jako pohyb soustavy dvou hmotných bodů – jde o tzv. problém dvou těles. Tento problém je řešitelný a lze jej zredukovat na problém jednoho tělesa.
Pohyb obou těles se vztahuje buď k těžišti soustavy, které se prostorem vůči vzdáleným objektům pohybuje rovnoměrně přímočaře (bez zrychlení), nebo k jednomu z těles, zpravidla k tomu hmotnějšímu. Jsou-li r1 a r2 polohové vektory prvního a druhého tělesa s počátkem v hmotnostním středu soustavy (těžišti), pak platí:
Lze dokázat, že trajektorie obou těles vzhledem k těžišti jsou podobné elipsy (se stejnou číselnou výstředností e), v jejichž jednom společném ohnisku leží těžiště systému. Jak plyne z výše uvedeného vztahu leží obě elipsy v téže rovině, přičemž velké poloosy těchto elips jsou kolineární a opačně orientované. Pro délku velkých poloos těchto elips a1 a a2 platí:
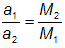
V praxi se pozorování dvojhvězd provádí takřka výhradně relativně – poloha slabší složky se vztahuje vůči složce jasnější, která bývá zpravidla i hmotnější z obou komponent. Relativní trajektorie druhé složky má rovněž tvar elipsy o stejné číselné výstřednosti e jako trajektorie obou složek vztažené k těžišti, přičemž tentokrát bude jasnější složka (počátek souřadnic) v ohnisku této elipsy. Velká poloosa oběžné elipsy a je dána součtem obou dílčích poloos:
Oběžná perioda soustava P vyhovuje 3. Keplerovu zákonu ve tvaru:
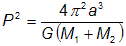
Pro periodu pak platí jednoduchý vztah:
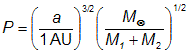 let.
let.
Tutéž periodu má těleso zanedbatelné hmotnosti pohybující se po elipse o velké poloose a kolem tělesa o hmotnosti M, kde M = M1+M2. Změřením oběžné doby P a velké poloosy relativní trajektorie jedné složky vůči druhé a tak lze vypočítat součet hmotností složek soustavy (ke zjištění hmotností jednotlivých složek je nutné navíc ještě znát alespoň poměr velkých poloos jejich drah a1/a2). Rovina trajektorie dvojhvězdy může být v prostoru vůči pozorovateli libovolně orientovaná. Tuto orientaci určuje úhel sklonu trajektorie i, což je úhel, který svírá normála k rovině trajektorie se směrem k pozorovateli. Je-li i = 0° nebo 180°, díváme se kolmo na trajektorii, je-li i blízké 90°, prohlížíme si soustavu z boku. Tehdy můžeme čas od času spatřit i zákryty složek soustavy. Další charakteristikou je orientace uzlové přímky, což je průsečnice roviny trajektorie s rovinou kolmou ke směru k pozorovateli, procházející počátkem (jednou z hvězd nebo těžištěm). Běžně se udává tzv. poziční úhel uzlové přímky, což je úhel, jenž svírá uzlová přímka s hlavní kružnicí procházející oběma póly a počátkem. Průměty trajektorií do roviny kolmé ke směru k pozorovateli dále zůstávají elipsami, jejichž výstřednost (excentricita) je obecně odlišná od vlastní excentricity trajektorie. V případě relativní trajektorie obecně neplatí, že by měla jasnější složka ležet v ohnisku elipsy. Nicméně z polohy výchozí složky vůči pozorované oběžné elipse lze vypočítat jak úhel sklonu trajektorie dvojhvězdy i, tak i polohu uzlové přímky a skutečnou excentricitu trajektorie podvojného systému e. Dále lze určit i ty body na oběžné dráze, v nichž se složky k sobě maximálně přiblíží (periastrum) nebo se od sebe naopak nejvíce vzdálí (apastrum). Polovina pozorované úhlové vzdálenosti apastra a periastra α' pak souvisí s úhlem α, pod nímž bychom viděli kolmo k nám postavenou velkou poloosu relativní trajektorie a. Je-li i’ úhel který mezi sebou svírají přímka apsid a směr k pozorovateli pak zřejmě platí:
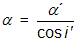 .
.
Poslední informací, která nám umožňuje vypočítat předpověď vzájemné polohy složek je okamžik průchodu periastrem, v kterémžto okamžiku jsou obě složky v prostoru k sobě nejblíže.