Centrální tlak a teplota
| Centrální tlak pc | Centrální teplota Tc |
Fyzikální podmínky v nitru hvězd
Ve stabilní hvězdě musí platit v každém místě jejího nitra rovnováha mezi gravitační silou a silou vztlakovou. Říkáme, že hvězda je v hydrostatické rovnováze. Na vztlakové síle se podílí zejména tlak plynu. V nitru velmi žhavých hvězd se uplatní také tlak záření.
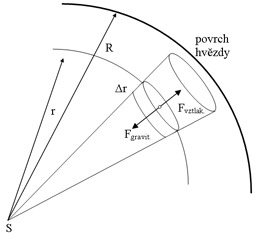
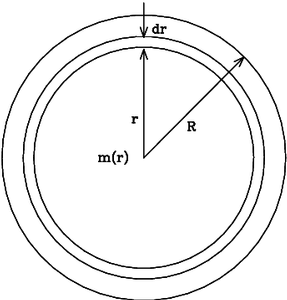
Budeme uvažovat malý váleček v nitru hvězdy, který je vzdálen r od jejího středu S, má podstavu o obsahu ΔS a malou výšku Δr. Plyn, který je v něm obsažený, má hustotu ρ(r) a hmotnost ρ(r)ΔSΔr. Tento váleček je přitahován do středu hvězdy pouze koulí o poloměru r a hmotnosti M(r), protože gravitační síly vrstev vyšších než r se navzájem ruší.
 |
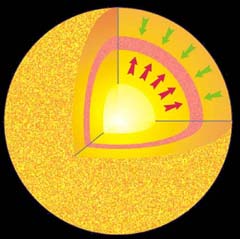 |
Ilustrační obrázek k rovnice hydrostatické rovnováhy hvězdného nitra |
Mechanická rovnováha ve hvězdě = platnost rovnice
hydrostatické rovnováhy a rovnice kontinuity
současně, tzn. dM/dr = 4πr2ρ. |
Gravitační síla působící na váleček má velikost
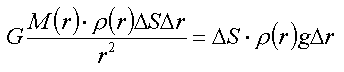 |
(1) |
a způsobuje zvýšení tlaku na spodní podstavu o Δp; přičemž
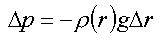 |
(2) |
kde G je gravitační konstanta G = 6,6742.10-11 m3.s-2.kg-1
Vztah (2) je nazýván rovnicí hydrostatické rovnováhy a vyjadřuje skutečnost, že
tlak p(r) roste spojitě od povrchu do centra hvězdy. Při zvětšení poloměru myšlené
koule o Δr přibude její hmotnost o ΔM(r), tedy o hmotnost
kulové slupky s poloměrem r a tloušťkou Δr
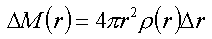 |
(3) |
Integrací rovnice (3) získáme hmotnost M(r) koule o poloměru r. Ve hvězdném nitru však zatím průběh hustoty neznámě, a proto nahradíme hustotu ρ(r) střední hodnotou hustoty ρ, kterou lze stanovit z objemu a hmotnosti hvězdy.
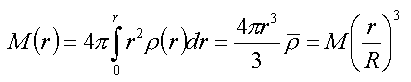 |
(4) |
Ve hvězdě působí tlak plynu pE
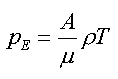 |
(5) |
kde A je plynová konstanta A = 8,31.10-3 J.kg.K-1, μ je střední hmotnost připadající na jednu částici.
U hvězd horní části hlavní posloupnosti působí tlak záření pr
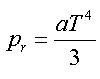 |
(6) |
kde a = 7,55.10-16 J.m-3.K-4.
Centrální tlak
Hodnotu centrálního tlaku pc odhadneme na základě výše uvedených vztahů. Tlak záření pr budeme zanedbávat, neboť je pro hvězdy s hmotnostmi srovnatelnými s hmotností Slunce mnohem menší než tlak plynu pE.
Vyjdeme z rovnice hydrostatické rovnováhy zapsané zjednodušeně p = pE. Tuto podmínku si lze představit tak, že tlak plynu v blízkosti středu plynné koule se musí rovnat tlaku vytvářenému tíhou sloupce plynu s příčným průřezem 1 m2 a výškou rovnou poloměru koule – hvězdy. Tíha sloupce plynu je rovna síle, kterou je přitahována ke středu koule. Dosadíme do zákona všeobecné gravitace
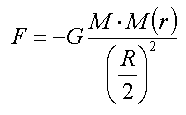 |
(7) |
kde M je hmotnost celé koule a M(r) je hmotnost výše definovaného sloupce plynu. Označíme-li symbolem ρ průměrnou hustotu plynu v sloupci, pak M(r) = ρR, kde R je poloměr koule. Vzdálenost mezi středy koule a sloupce plynu je r = R/2. Za těchto podmínek je tíha vytyčeného sloupce plynu na 1 m2 rovna
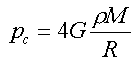 |
(8) |
Po dosazení základních charakteristik Slunce,
M = 2.1030 kg, R = 7.108 m,
ρ = 1,4.103 kg.m-3 obdržíme
pc ≈ 1015 N.m-2.
Vzhledem ke značné teplotě je i při tak vysokém tlaku látka ve slunečním centru stále ve stavu plynu.
Centrální teplota
Pro výpočet průměrné teploty v nitru hvězdy Tc budeme předpokládat, že přibližně platí p = pc/2, kde p je průměrný tlak ve vzdálenosti r = R/2 od středu hvězdy. Dosazením do vztahu pro tlak obdržíme
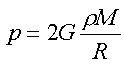 |
(9) |
Ze stavové rovnice vyjádříme
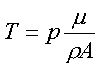 |
(10) |
a po úpravě dostaneme
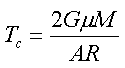 |
(11) |
Po dosazení hodnot pro Slunce, μ = 0,6 získáme
T ≈ 107 K.
Takto vysoká teplota vypovídá o plazmovém stavu hvězdy. Postupnou přeměnou vodíku na helium
se pozvolna zvyšuje střední hmotnost částic plynu a mění se také hustota ρ.
Chemické změny v nitru hvězdy nutně vedou ke zvyšování centrální teploty Tc.